STRUKTUR DATA
Fungsi Rekursif
Jumat, 06 April 2012
Fungsi Rekursif
Fungsi rekursif adalah suatu fungsi yang memanggil dirinya sendiri. Pada beberapa persoalan,fungsi rekursif sangat berguna karena mempermudah solusi. Namun demikian, fungsi rekursif juga memiliki kelemahan, yakni memungkinkan terjadinya overflow pada stack, yang berarti stack tidak lagi mampu menangani permintaan pemanggilan fungsi karena kehabisan memori( stack adalah area memori yang dipakai untuk variable lokal untuk mengalokasikan memori ketika suatu fungsi di panggil. Oleh karena itu, jika bisa diselesaikan dengan metode iteratif, gunakanlah metode iteratif.
Fungsi rekursif dapat digunakan untuk menghitung faktorial. Berikut penjelasan beserta dengan contoh listing programnya.
Fungsi faktorial dapat dinyatakan dalam bentuk rekursif seperti berikut:
fak(n) = 1, untuk n = 0 atau n = 1
fak(n) = n x (n-1)!, untuk n > 0
contoh coding :
import javax.swing.JOptionPane;
public class kacong {
public static void f(int d) {
int hasil =1;
for (;d>=1;d--)
hasil = hasil*d;
System.out.println("faktor = "+hasil);
}
public static int faktorial (int x) {
if (x==0)
return 1;
return (x*faktorial(x-1));
}
public static void main (String []args){
kacong.f(Integer.parseInt(JOptionPane.showInputDialog("Masukkan Bilangan faktorial")));
}
}
FLOWCHART
KESIMPULAN
Fungsi rekursif adalah suatu fungsi yang memanggil dirinya sendiri. Pada beberapa persoalan,fungsi rekursif sangat berguna karena mempermudah solusi
Fungsi faktorial dapat dinyatakan dalam bentuk rekursif seperti berikut:
fak(n) = 1, untuk n = 0 atau n = 1
fak(n) = n x (n-1)!, untuk n > 0
Pengertian Array
Array (larik) merupakan tipe data tersetruktur dimana didalamnya terdiri dari komponen – komponen yang mempunyai tipe data yang sama. Didalam suatu array jumlah komponen banyaknya adalah tetap. Didalam suatu larik atau array setiap kompoenen ditunjukan oleh suatu index yang unik. Index dari setiap komponen array menunjukan urutan data atau identitas yang mewakili data yang ada didalamnya.
Logika sederhananya array itu bisa disamakan dengan dua orang dengan nama yang sama didalam suatu komunitas, untuk membedakan antara nama yang satu atau dengan nama yang lain maka diberikan initial tambahan untuk setiap nama.
Deklarasi Array
Didalam penulisan bahasa pemograman setiap penggunaan array harus dideklarsikan terlebih dahulu. Pendeklarasian array diawali dengan nama variabel array diikuti dengan indeks array yang dituliskan didalam tanda “[]” , diikuti dengan kata cadangan of dan tipe data yang dibutuhkan.
Bentuk Umum Penulisan
Tanda_pengenal : array [..tipe index ..] of tipe data;
Contoh :
Var
A : array[1..4] of integer;
B : array[1..5] of string;
C: array[1..10] of real;
Keterangnan :
A,B,C merupakan tanda pengenal/ nama variabel dari array;
1..4 : merupakan tipe indek dari array, yang menunjukan banyaknya data yang mampu disimpan.
Integer : menunjukan bahwa data yang diinput berupa bilangan bulat.
Tower of Hanoi
Tower of Hanoi adalah sebuah permainan matematik. Permainan ini terdiri dari tiga tiang dan sejumlah cakram yang berbeda ukuran yang dapat dipindah-pindahkan dari tiang satu ketiang lainnya. Permainan dimulai dengan setumpukan cakram di tiang pertama (S), dengan cakram terbesar dibagian bawah dan cakram terkecil dibagian atas.
Tujuan permainan ini adalah memindahkan seluruh cakaram yang berada di tiang S (Source) ke tiang D (Destination), tiang I (Intermediate) sebagai perantara.
Ketentuan/ aturan permainannya adalah sebagai berikut:
---Hanya satu cakram yang boleh dipindahkan dalam satu waktu.
---Setiap perpindahan berupa pengambilan cakram teratas dari satu tiang dan memindahkannya ketiang lain yang mungkin belum atau sudah berisi cakram lain.
---Cakram yang ukurannya lebih besar, tidak boleh berada diatas cakram yang ukurannya lebih kecil.
Teka-teki ini ditemukan Édouard Lucas, ahli matematika Perancis di tahun 1883. Ada sebuah legenda tentang candi Indian yang berisi ruang besar dengan tiga tiang yang dikelilingi 64 cakram emas. Pendeta Brahma, melaksanakan tugas dari peramal di masa lalu, sesuai dengan aturan teka-teki ini. Menurut legenda ini, bila teka-teki ini diselesaikan, dunia akan kiamat. Tidak jelas benar apakah Lucas menemukan legenda ini atau terinspirasi olehnya.
Bila legenda ini benar, dan pendeta itu bisa memindahkan satu cakram tiap detik, menggunakan pemindahan paling sedikit, maka akan memakan waktu 264−1 detik atau kurang lebih 584,582 milyar tahun.
Permainan Menara Hanoi sering digunakan dalam penelitian psikologis dalam hal pemecahan masalah. Selain itu, juga sering digunakan dalam pengajaran algorima rekursif bagi pelajar pemrograman. Permainan ini juga digunakan sebagai ujian ingatan oleh ahli psikolog syaraf dalam berupaya mengevaluasi amnesia.
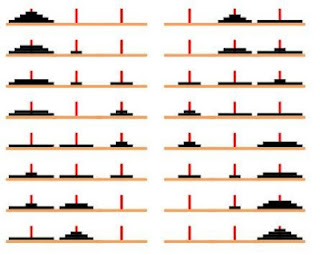
Contoh gambar Tower Of Hanoi
Tower of Hanoi adalah sebuah permainan matematik. Permainan ini terdiri dari tiga tiang dan sejumlah cakram yang berbeda ukuran yang dapat dipindah-pindahkan dari tiang satu ketiang lainnya. Permainan dimulai dengan setumpukan cakram di tiang pertama (S), dengan cakram terbesar dibagian bawah dan cakram terkecil dibagian atas.
Tujuan permainan ini adalah memindahkan seluruh cakaram yang berada di tiang S (Source) ke tiang D (Destination), tiang I (Intermediate) sebagai perantara.
Ketentuan/ aturan permainannya adalah sebagai berikut:
---Hanya satu cakram yang boleh dipindahkan dalam satu waktu.
---Setiap perpindahan berupa pengambilan cakram teratas dari satu tiang dan memindahkannya ketiang lain yang mungkin belum atau sudah berisi cakram lain.
---Cakram yang ukurannya lebih besar, tidak boleh berada diatas cakram yang ukurannya lebih kecil.
Teka-teki ini ditemukan Édouard Lucas, ahli matematika Perancis di tahun 1883. Ada sebuah legenda tentang candi Indian yang berisi ruang besar dengan tiga tiang yang dikelilingi 64 cakram emas. Pendeta Brahma, melaksanakan tugas dari peramal di masa lalu, sesuai dengan aturan teka-teki ini. Menurut legenda ini, bila teka-teki ini diselesaikan, dunia akan kiamat. Tidak jelas benar apakah Lucas menemukan legenda ini atau terinspirasi olehnya.
Bila legenda ini benar, dan pendeta itu bisa memindahkan satu cakram tiap detik, menggunakan pemindahan paling sedikit, maka akan memakan waktu 264−1 detik atau kurang lebih 584,582 milyar tahun.
Permainan Menara Hanoi sering digunakan dalam penelitian psikologis dalam hal pemecahan masalah. Selain itu, juga sering digunakan dalam pengajaran algorima rekursif bagi pelajar pemrograman. Permainan ini juga digunakan sebagai ujian ingatan oleh ahli psikolog syaraf dalam berupaya mengevaluasi amnesia.
Contoh gambar Tower Of Hanoi
Contoh coding:
import java.io.*;
import java.lang.*;
import java.util.*;
class TowerOfHanoi
{
static int movecount = 0;
static public void Solve2DiscsTOH(Stack source, Stack temp, Stack dest)
{
temp.push(source.pop());
movecount++;
PrintStacks();
dest.push(source.pop());
movecount++;
PrintStacks();
dest.push(temp.pop());
movecount++;
PrintStacks();
}
static public int SolveTOH(int nDiscs, Stack source, Stack temp, Stack dest)
{
if (nDiscs <= 4)
{
if ((nDiscs % 2) == 0)
{
Solve2DiscsTOH(source, temp, dest);
nDiscs = nDiscs - 1;
if (nDiscs == 1)
return 1;
temp.push(source.pop());
movecount++;
PrintStacks();
//new source is dest, new temp is source, new dest is temp;
Solve2DiscsTOH(dest, source, temp);
dest.push(source.pop());
movecount++;
PrintStacks();
//new source is temp, new temp is source, new dest is dest;
SolveTOH(nDiscs, temp, source, dest);
}
else
{
if (nDiscs == 1)
return -1;
Solve2DiscsTOH(source, dest, temp);
nDiscs = nDiscs - 1;
dest.push(source.pop());
movecount++;
PrintStacks();
Solve2DiscsTOH(temp, source, dest);
}
return 1;
}
else if (nDiscs >= 5)
{
SolveTOH(nDiscs - 2, source, temp, dest);
temp.push(source.pop());
movecount++;
PrintStacks();
SolveTOH(nDiscs - 2, dest, source, temp);
dest.push(source.pop());
movecount++;
PrintStacks();
SolveTOH(nDiscs - 1, temp, source, dest);
}
return 1;
}
static public Stack A = new Stack();
static public Stack B = new Stack();
static public Stack C = new Stack();
static public void PrintStacks()
{
if (countA != A.size() ||
countB != B.size() ||
countC != C.size())
{
int diffA = A.size() - countA;
int diffB = B.size() - countB;
int diffC = C.size() - countC;
if (diffA == 1)
{
if (diffB == -1)
System.out.print("Move Disc " + A.peek() + " From B To A");
else
System.out.print("Move Disc " + A.peek() + " From C To A");
}
else if (diffB == 1)
{
if (diffA == -1)
System.out.print("Move Disc " + B.peek() + " From A To B");
else
System.out.print("Move Disc " + B.peek() + " From C To B");
}
else //if (diffC == 1)
{
if (diffA == -1)
System.out.print("Move Disc " + C.peek() + " From A To C");
else
System.out.print("Move Disc " + C.peek() + " From B To C");
}
countA = A.size();
countB = B.size();
countC = C.size();
System.out.println();
}
PrintStack(A);
System.out.print(" , ");
PrintStack(B);
System.out.print(" , ");
PrintStack(C);
System.out.print(" , ");
}
static int countA = 0;
static int countB = 0;
static int countC = 0;
static public void PrintStack(Stack s)
{
System.out.print(s.toString());
}
public static void main(String[] args)
{
try
{
while (true)
{
System.out.print("\nEnter the number of discs (-1 to exit): ");
int maxdisc = 0;
String inpstring = "";
InputStreamReader input = new InputStreamReader(System.in);
BufferedReader reader = new BufferedReader(input);
inpstring = reader.readLine();
movecount = 0;
maxdisc = Integer.parseInt(inpstring);
if (maxdisc == -1)
{
System.out.println("Good Bye!");
return;
}
if (maxdisc <= 1 || maxdisc >= 10)
{
System.out.println("Enter between 2 - 9");
continue;
}
for (int i = maxdisc; i >= 1; i--)
A.push(i);
countA = A.size();
countB = B.size();
countC = C.size();
PrintStacks();
SolveTOH(maxdisc, A, B, C);
System.out.println("Total Moves = " + movecount);
while (C.size() > 0)
C.pop();
}
}
catch (Exception e)
{
e.printStackTrace();
}
}
}
http://tlpuzzle.weebly.com/tower-of-hanoi.html
http://id.wikipedia.org/wiki/Menara_Hanoi










0 komentar:
Posting Komentar
Komentar Anda mengenai Postingan ini sangat Saya butuhkan Untuk menjadi bahan evaluasi agar menjadi lebih baik.....